Học Máy Liên Kết: Tổng Quan

Posted Aug 15, 2024

By Anh Dinh 15 min read

Nội dung

1. Giới thiệu
2. Các đặc điểm chính của học liên kết
3. Các loại học liên kết dựa trên đặc điểm phân phối của dữ liệu
4. Thuật toán của học liên kết
5. Các biến thể của học liên kết
6. Tham khảo

1. Giới thiệu

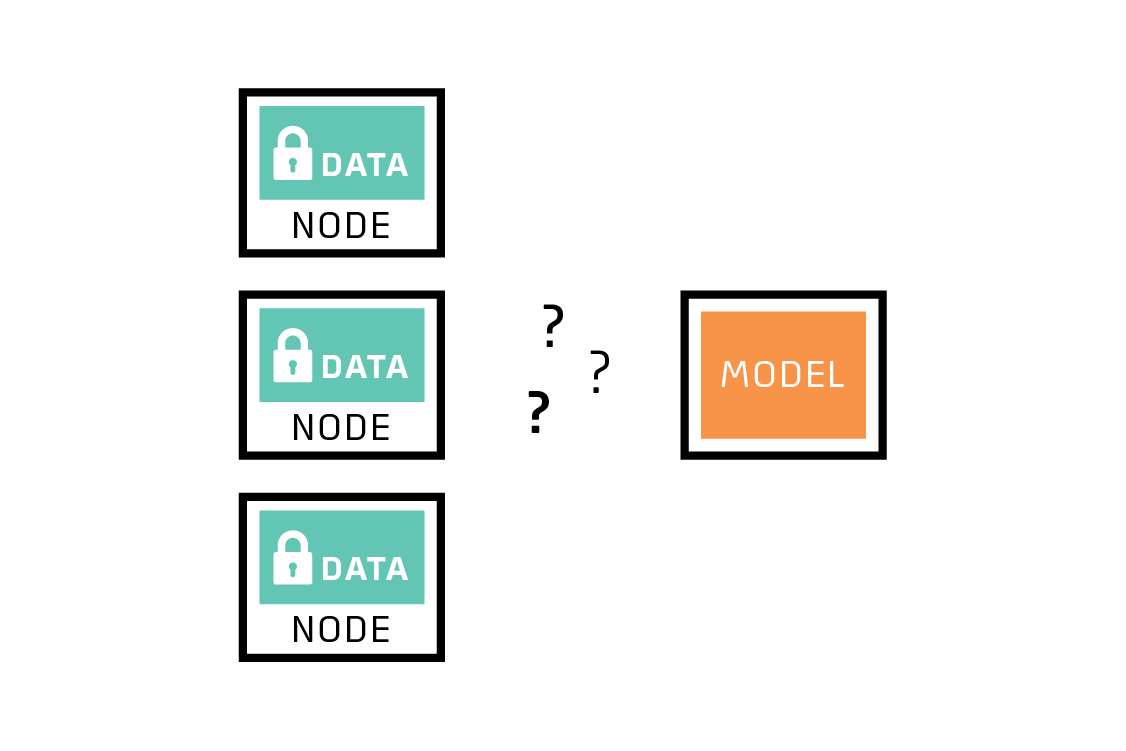
Hiện nay, việc huấn luyện các mô hình trí tuệ nhân tạo với phương pháp Học máy cổ điển đang phải đối mặt với hai thử thách chính. Một là trong hầu hết các ngành công nghiệp dữ liệu thường bị cô lập, phân tán nhiều nơi. Hai là ngày càng nhiều các chính sách bảo mật dữ liệu. Để giải quyết những khó khăn này một phương pháp học máy với phân tán mới đã được các kỹ sư của Google đề xuất [1].

Học liên kết hay còn được gọi là học cộng tác là một kỹ thuật Học máy cho phép huấn luyện mô hình trí tuệ nhân tạo với dữ liệu trên các thiết bị, máy chủ, trung tâm dữ liệu phân tán mà không cần phải tập trung dữ liệu lại một nơi như cách chúng ta thường làm với phương pháp Học máy cổ điển nhưng vẫn có hiệu suất không quá khác biệt so với phương pháp học máy cổ điển [1][2].

2. Các đặc điểm chính của học liên kết

2.1 Iterative learning

Để đảm bảo kết quả cuối cùng của mô hình toàn cục có kết quả tốt, Học liên kết học tập dựa vào quá trình lặp được chia nhỏ thành một tập hợp các tương tác giữa Node và Server gọi là vòng lặp học liên kết. Mỗi quy trình vòng lặp bao gồm việc gửi mô hình toàn cục cho các Node tham gia huấn luyện với dữ liệu cục bộ để tạo ra mô hình cục bộ và tổng hợp các mô hình cục bộ này để tạo phiên bản mô hình toàn cục mới [3].

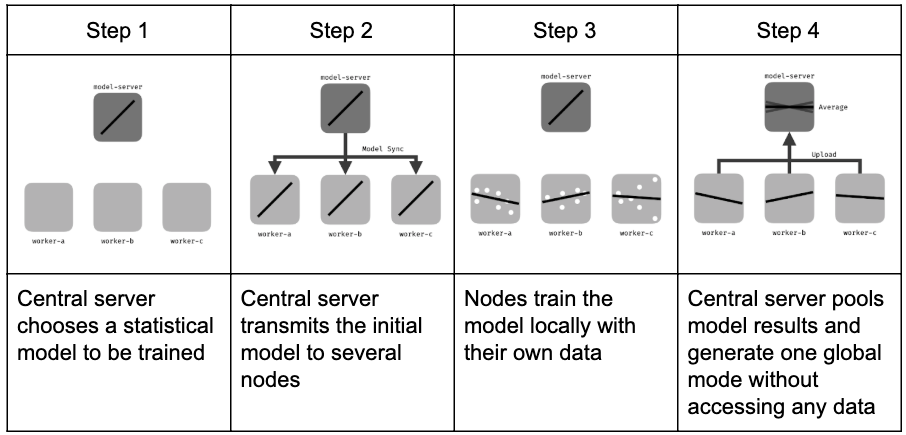Hình 1. Các quy trình chính của Học liên kết.

Quá trình lặp học liên kết gồm các quy trình chính như sau [4]:

Khởi tạo: Dựa trên tập nhỏ dữ liệu ở Server, một mô hình học máy được chọn và huấn luyện bước đầu.
Chọn các Node học: Một tỉ lệ các Node (tập con của toàn bộ Node đang tham gia học) sẽ được chọn để tham gia vào quá trình huấn luyện. Các Node không được chọn khác thì đợi các vòng lặp sau.
Cấu hình: Server sẽ gửi các siêu tham số cho các Node để huấn luyện với dữ liệu cục bộ (mini_batch, local_iteration, v.v.).
Phản hồi: Các Node sau khi học sẽ gửi mô hình cục bộ trở lại Server để tiến hành tổng hợp. Server sẽ tổng hợp các kết quả này lại tạo phiên bản mô hình toàn cục mới. Đối với các Node được chọn nhưng bị lỗi (mất kết nối, v.v.) không phản hồi được ở vòng này thì sẽ được yêu cầu gửi phản hồi ở các vòng lặp sau.
Kết thúc: Một khi đạt được kết quả mong đợi (số vòng lặp toàn cục hoặc là một ngưỡng hiệu suất cụ thể) thì Server sẽ hoàn thiện mô hình toàn cục và kết thúc quá trình lặp.

2.2 Dữ liệu non-IID

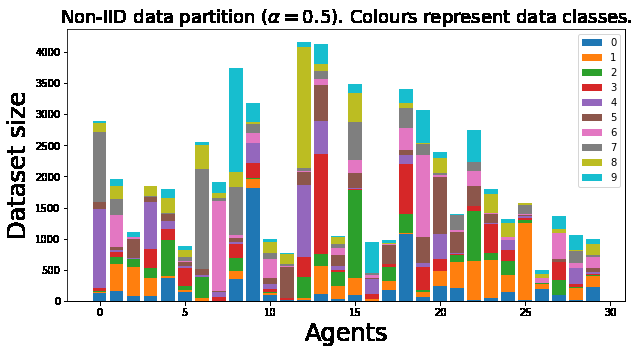Hình 2. Ví dụ về một trường hợp dữ liệu non-IID.

Thông thường, dữ liệu phân bố phân tán trên các Node là dữ liệu non-IID (dữ liệu không đồng nhất hoặc phân phối không độc lập). Dữ liệu non-IID được mô tả dựa trên phân tích xác suất hợp giữa các feature và label của mỗi Node. Điều này cho phép tách từng đóng góp theo phân phối cụ thể có sẵn tại các Node cục bộ. Dữ liệu non-IID có những đặc tính chính như sau [3]:

Covariate shift: Các Node cục bộ có thể lưu trữ các ví dụ có phân phối thống kê khác so với các Node khác. Ví dụ cho trường hợp này là thường mọi người viết chữ thì độ rộng nét hoặc độ nghiêng sẽ khác nhau.
Prior probability shift: Các Node cục bộ có thể lưu trữ các label khác nhau. Điều này có thể xảy ra nếu các bộ dữ liệu được phân theo khu vực hoặc theo vùng miền. Ví dụ như là bộ dữ liệu chứa hình ảnh động vật khác nhau đáng kể giữa các quốc gia.
Concept drift: Các Node cục bộ có thể có cùng label nhưng các feature của chúng lại không giống nhau.
Concept shift: Các Node cục bộ có thể có cùng các feature nhưng label của chúng lại không giống nhau.
Unbalancedness: Lượng dữ liệu có sẵn tại các Node cục bộ có thể khác nhau về kích thước.

2.3 Tính bảo mật

Hình 3. Tính bảo mật dữ liệu.

Bảo mật là ưu tiên số một của học liên kết. Trong điều kiện quyền riêng tư dữ liệu ngày càng được chú trọng, nhiều chính sách về bảo vệ quyền riêng tư dữ liệu đã được đưa ra [5]. Để học máy có thể phát huy tiềm năng mà vẫn đảm bảo được an toàn dữ liệu là mục tiêu chính của học liên kết.

Ý tưởng chính của học liên kết là huấn luyện mô hình với dữ liệu cục bộ và chỉ trao đổi các tham số cập nhật mô hình. Điều này giúp dữ liệu được bảo vệ trọn vẹn ở phía node cục bộ, không bị rò rỉ dữ liệu mà vẫn tham gia được vào quá trình học chung với các node khác [1].

3. Các loại học liên kết dựa trên đặc điểm phân phối của dữ liệu

Trong học liên kết, dữ liệu thường có phân phối và đặc tính rất đa dạng. Để phù hợp với các bài toán khác nhau, chúng ta có các hình thức học liên kết dựa trên phân vùng và đặc tính của dữ liệu [1].

Một số ký hiệu:

$i$ là node thứ $i$ trong $\{1, \ldots, N\}$ node
$D_i$ ký hiệu là ma trận dữ liệu tại node sở hữu $i$
$X_i$ là feature space của node thứ $i$
$Y_i$ là label space của node thứ $i$
$I$ ký hiệu cho ID space
Một tập dữ liệu tại một node sẽ như thế này $(I, X, Y)$

3.1 Học liên kết dọc

Hình 4. Học liên kết dọc.

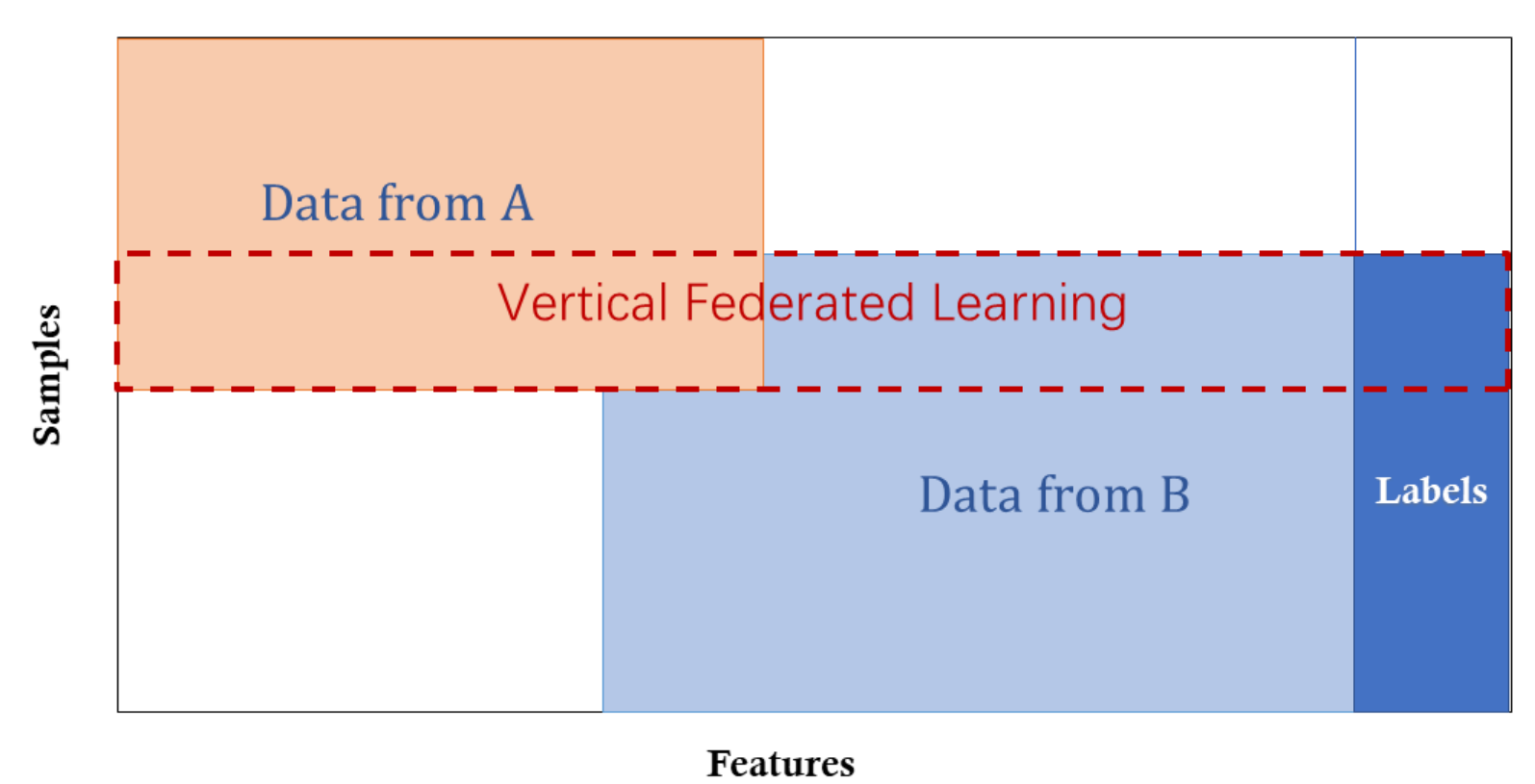
Học liên kết dọc còn được gọi là học liên kết dựa trên feature, áp dụng cho các trường hợp hai bộ dữ liệu có chung (ID space) nhưng khác nhau về (feature space). Ví dụ, trong trường hợp hai công ty khác nhau ở trong cùng một thành phố: một bên là ngân hàng và bên còn lại là một sàn thương mại điện tử. Khách hàng của họ có khả năng cao là những cư dân trong thành phố nên có thể có nhiều khách hàng chung. Tuy nhiên, ngân hàng ghi lại hành vi chi tiêu và xếp hạng tín dụng của khách hàng, còn sàn thương mại điện tử ghi lại lịch sử tìm kiếm và mua sắm của khách hàng, vì vậy các feature của họ rất khác nhau. Giả sử chúng ta muốn cả hai bên có mô hình dự đoán mua đồ dựa trên thông tin khách hàng và thông tin sản phẩm [1].

Học liên kết dọc là quá trình tổng hợp các feature khác nhau và huấn luyện mô hình dựa trên loss và gradient một cách riêng tư giữa hai bên hợp tác. Với cách học này, danh tính và tình trạng của mỗi bên tham gia là như nhau và hệ thống liên bang giúp thiết lập một mô hình chung. Trong hệ thống này, chúng ta có những tính chất sau [1]:

\[X_i \neq X_j, \quad Y_i \neq Y_j, \quad I_i = I_j, \quad \forall D_i, D_j, \, i \neq j\]

3.2 Học liên kết ngang

Hình 5. Học liên kết ngang.

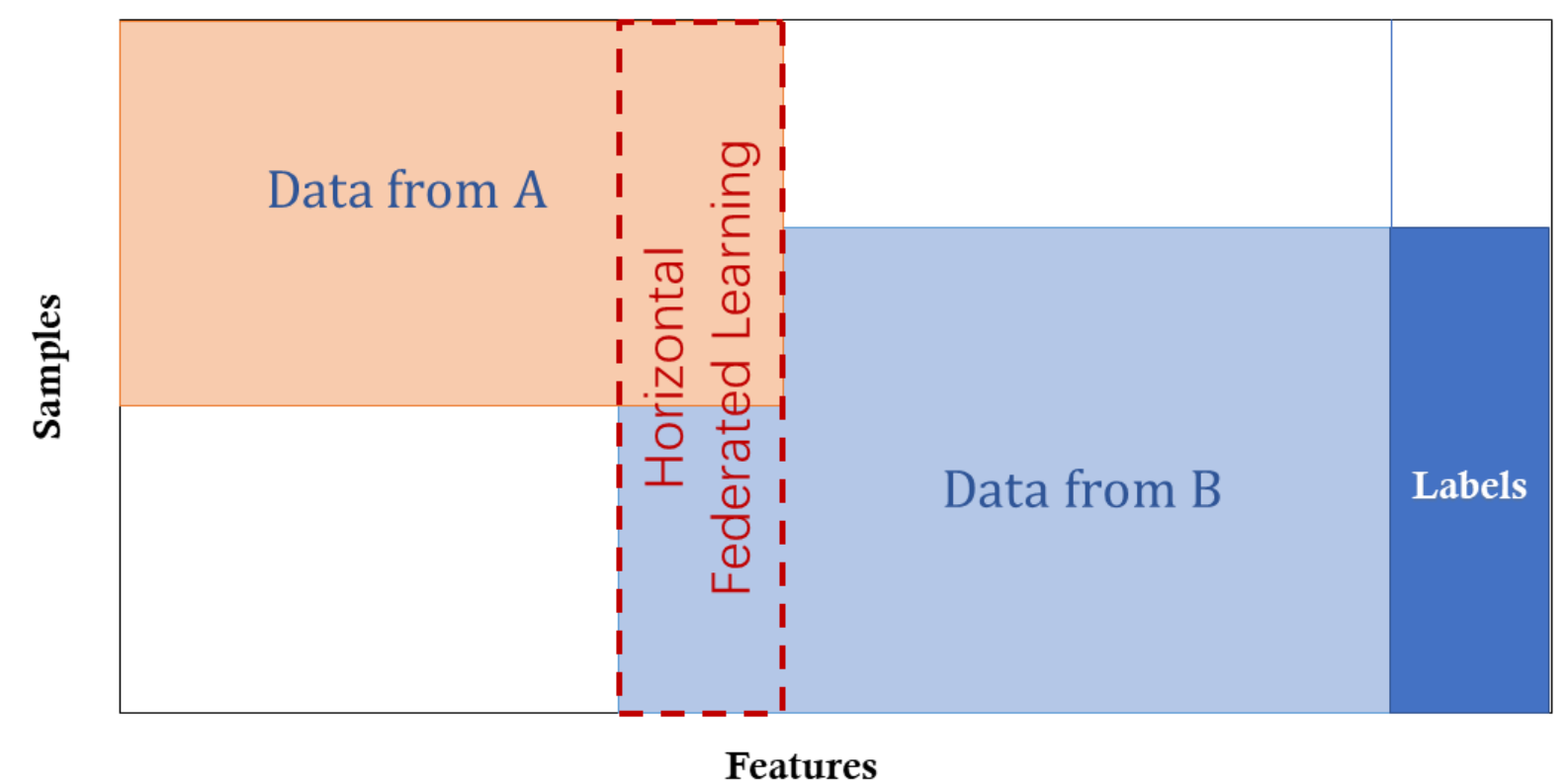
Học liên kết ngang còn được gọi là học liên kết dựa trên mẫu, có nghĩa là trong trường hợp này feature space sẽ như nhau và hai bên học sẽ tiến hành đóng góp thêm mẫu để làm giàu dữ liệu. Ví dụ, chúng ta có hai ngân hàng khu vực có các nhóm khách hàng khác nhau trong các khu vực tương ứng và số lượng khách hàng chung rất ít. Tuy nhiên, hoạt động kinh doanh của họ rất giống nhau, vì vậy feature space sẽ giống nhau. Một ví dụ khác là vào năm 2017 Google đã đề xuất học liên kết ngang như là một giải pháp cập nhật tham số mô hình cho điện thoại Android. Trong giải pháp này, một khách hàng sử dụng điện thoại Android sẽ cập nhật tham số mô hình cục bộ của họ và tải những tham số này lên đám mây của Android, cùng nhau đào tạo mô hình học liên kết tập trung với các thiết bị Android khác. Trong hệ thống học này, chúng ta có những đặc điểm sau [1]:

\[X_i = X_j, \quad Y_i = Y_j, \quad I_i \neq I_j, \quad \forall D_i, D_j, \, i \neq j\]

3.3 Học liên kết chuyển giao

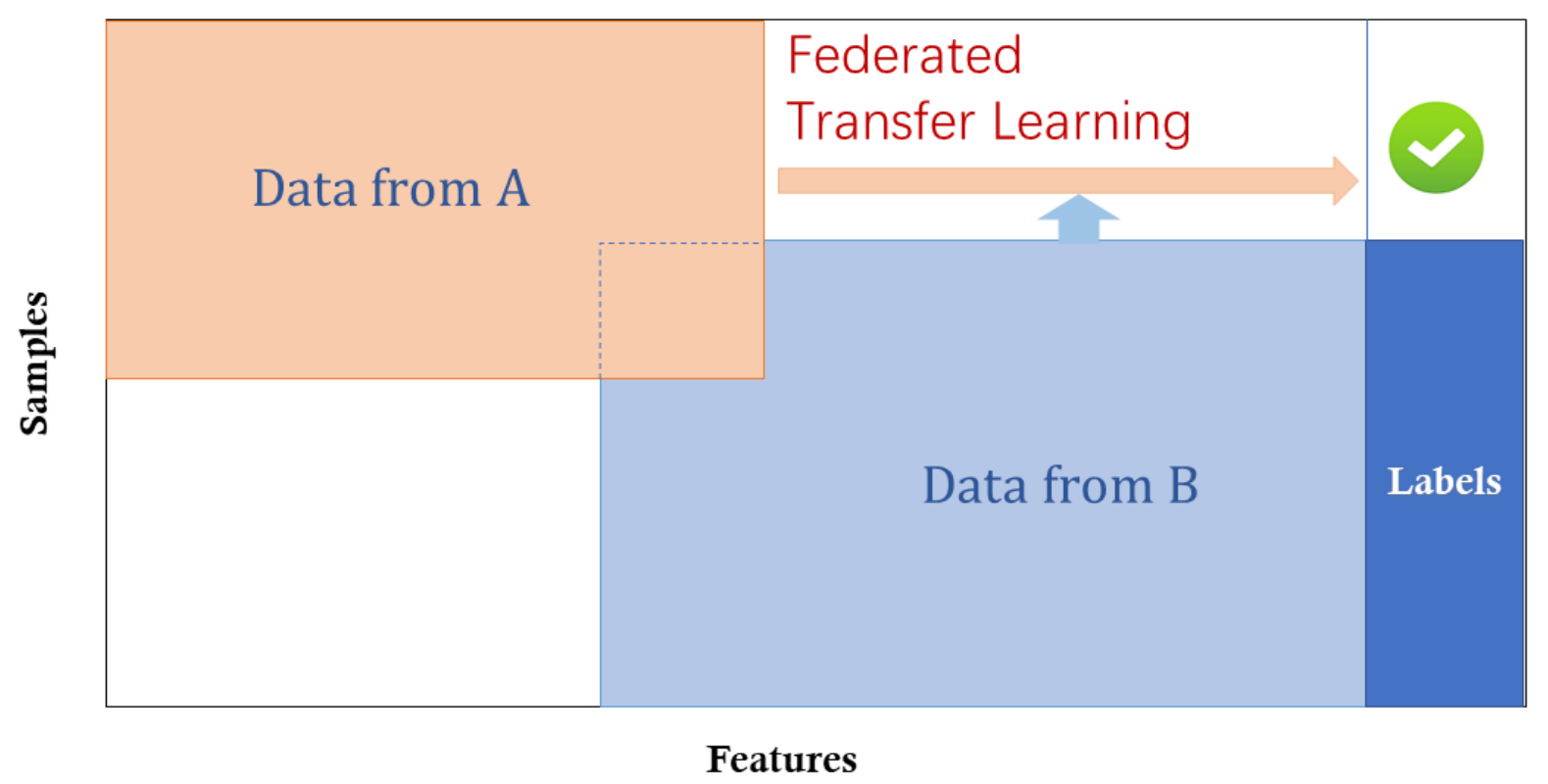Hình 6. Học liên kết chuyển giao.

Học liên kết chuyển giao có phần đặc biệt hơn so với học liên kết ngang và học liên kết dọc, đó là hai tập dữ liệu khác nhau sẽ không có bất cứ điểm chung nào trong feature space và sample space. Ví dụ như có hai doanh nghiệp, một bên là một ngân hàng nội địa tại Việt Nam và một bên là một sàn thương mại điện tử tại Mỹ. Bởi vì giới hạn về mặt địa lý, các nhóm khách hàng của hai doanh nghiệp này có rất ít khách hàng chung. Bên cạnh đó, hoạt động kinh doanh khác nhau nên có rất ít feature space chung. Trong trường hợp này, kỹ thuật học liên kết chuyển giao có thể được áp dụng để cung cấp giải pháp cho feature space và sample space để học liên kết. Học liên kết chuyển giao là một tính năng quan trọng của học liên kết, ở kỹ thuật học này chúng ta có những đặc điểm sau [1]:

\[X_i \neq X_j, \quad Y_i \neq Y_j, \quad I_i \neq I_j, \quad \forall D_i, D_j, \, i \neq j\]

4. Thuật toán của học liên kết

Trong quá trình học tập liên kết, chúng ta có thể kiểm soát các tham số khác nhau của việc học để tối ưu hóa việc học. Học liên kết có một vài tham số chính như sau:

$T$ là số vòng lặp của học liên kết (global iteration)
$K$ là tổng số Node tham gia quá trình học
$C$ là tỉ lệ một phần các Node được chọn cho một vòng lặp của học liên kết
$B$ là batch size cục bộ của các Node tham gia vào vòng lặp của học liên kết

Một số tham số cho mô hình:

$N$ là số vòng lặp cục bộ của các Node tham gia trước khi gửi kết quả về Server
$\eta$ là learning rate
$\mu$ là tham số phạt

Một số ký hiệu trong các công thức của thuật toán:

$k$ là chỉ mục của tập hợp tất cả các Node tham gia
$n_k$ là số lượng dữ liệu tại Node $k$
$\theta_{k,t}$ là mô hình của Node $k$ tại vòng lặp học liên kết $t$
$l(w, b)$ là hàm loss với tham số weights và bias của mô hình
$E$ là số lượng vòng lặp cục bộ

Mục tiêu của Học liên kết là đào tạo mô hình toàn cục với hiệu suất cao nhất trên tất cả các Node, do đó hàm mục tiêu của Học liên kết sẽ là [6]:

\[\min f(w) \text{ where } w \in \mathbb{R}^d, \quad f(w) = \frac{1}{n} \sum_{i=1}^n f_i(w) \quad (1)\]

Trong Học máy, chúng ta thường dùng ký hiệu $f_i(w) = l(x_i, y_i; w)$ để mô tả hàm loss của dự đoán $(x_i, y_i)$ với mô hình $w$. Giả định rằng có $K$ Node tham gia vào quá trình học, ký hiệu $P_k$ là dữ liệu tại phân vùng $k$, với $n_k = \lvert P_k \rvert$. Do đó chúng ta có thể viết lại công thức (1) như sau [6]:

\[f(w) = \frac{1}{n} \sum_{k=1}^K F_k(w) \text{ where } F_k(w) = \frac{1}{n_k} \sum_{i \in P_k} f_i(w) \quad (2)\]

Quy trình chính của Học liên kết:

$\textbf{ServerExecute:}$

Khởi tạo $w_0$
for $t \in T$ do:
- $m \leftarrow (C \cdot K, 1)$
- $S_t \leftarrow$ (một tập con ngẫu nhiên với $m$ node được chọn)
- for $k \in S_t$ parallel do:
  - $w_{t+1}^k \leftarrow \text{ClientUpdate}(k, w_t)$
- Tổng hợp phản hồi từ các Node để tạo $w_{t+1}$ (phiên bản mô hình toàn cục mới)

$\textbf{ClientUpdate}(k, w_t):$

$\beta \leftarrow$ chia nhỏ $P_k$ thành các batch con có kích thước $B$
for $i \in E$ do:
- For batch $b \in \beta$ do:
  - $w \leftarrow w - \eta \nabla l(w; b)$
Gửi $w$ về Server

5. Các biến thể của học liên kết

5.1 FedSGD

Về cơ bản, thuật toán tối ưu của Học liên kết được xây dựng dựa trên phương pháp giảm Gradient (SGD). Học liên kết dựa trên giảm Gradient (FedSGD) tính toán các Gradient theo từng batch (mỗi batch nghĩa là mỗi Node) trong một vòng lặp Học liên kết [6].

Các cài đặt thông thường khi chúng ta triển khai huấn luyện mô hình với phương pháp FedSGD là tỉ lệ $C = 1$, $B = \infty$, $E = 1$ và $\eta$ cố định. Các Node tính toán $g_k = \nabla F_k(w_t)$ và phản hồi $g_k$ cho Server. Sau đó, Server sẽ tổng hợp mô hình toàn cục mới theo công thức sau [6]:

\[w_{t+1} \leftarrow \nabla f(w_t) \quad \text{where} \quad \nabla f(w_t) = w_t - \eta \sum_{k=1}^{K} \frac{n_k}{n} g_k \quad (3)\]

Cách tiếp cận này có vẻ hiệu quả nhưng yêu cầu số lượng vòng lặp rất lớn để huấn luyện được một mô hình tốt [7].

5.2 FedAvg

Cách triển khai dựa trên giảm Gradient (3) còn có thể triển khai như sau: các Node tính toán $g_k$ và cập nhật cho mô hình cục bộ $w_{t+1}^k \leftarrow w_t - \eta g_k$ và sau đó phản hồi $w_{t+1}^k$ cho Server. Sau đó, Server sẽ tổng hợp mô hình toàn cục mới theo công thức sau:

\[w_{t+1}^k \leftarrow w_t - \sum_{k=1}^{K} \frac{n_k}{n} g_k \quad (4)\]

Khi chúng ta triển khai theo thuật toán này, chúng ta thấy là chúng ta đang tính trung bình các mô hình cục bộ nên phương pháp này gọi là Học liên kết AVG (FedAvg) [6].

Cách triển khai FedAvg sử dụng ba tham số chính là tỉ lệ các Node được chọn mỗi vòng lặp Học liên kết ($C$), số vòng lặp cục bộ ($E$) và local batch size ($B$). Khi chúng ta để $C = 1$, $B = \infty$, $E = 1$ sẽ tương đương với cách triển khai SGD. Với mỗi Node có $n_k$ dữ liệu thì số cập nhật mỗi vòng là $u_k = \frac{E \cdot n_k}{B}$ [6].

5.3 FedProx

Với thuật toán FedAvg, mỗi vòng lặp Học liên kết sẽ chọn một tỉ lệ $C$ (0 < $C$ < 1) Node để tham gia vào quá trình học. Các Node này sẽ tối ưu hóa mô hình cục bộ bằng phương pháp giảm Gradient, với tham số $E$ (local epoch) là cố định nên mô hình cục bộ sẽ được học $E$ lần [6]. Vì dữ liệu của các Node không giống nhau nên có thể sẽ có trường hợp có Node hội tụ sớm còn có Node thì chưa hội tụ. Không ít trường hợp mô hình cục bộ đã hội tụ sớm và tiếp tục lặp ra xa điểm hội tụ của mô hình toàn cục [8]. Để giảm thiểu vấn đề này, chúng ta sử dụng một tham số phạt là $\mu$ để kiểm soát sự chênh lệch khác nhau giữa $w_t$ và $w_{t+1}^k$. Hàm phạt sẽ được đưa vào chung với hàm loss cục bộ theo công thức sau [8]:

\[h(w; w_0) = F(w) + \frac{\mu}{2} \|w - w_0\|^2 \quad (5)\]